The Partitioned Boolean Quadratic Problem (PBQP) is an abstract optimization problem or more exactly a special case of a quadratic assignment problem (like the travelling salesman). Essentially, you have a multiple choice task with interdependencies.
What is a PBQP?
A nice representation is in a graph. Each node represents some options, where exactly one must be choosen. The edges represent the interdependencies. To assign costs, we annotate the nodes with cost vectors and the edges with cost matrices. Selecting options at two nodes implicitly selects the corresponding entry in the cost matrix between them.
The following figure presents the classical graph coloring problem with three nodes and three colors as a PBQP.
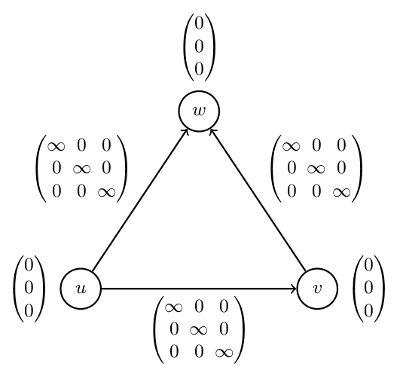
You can see that each of three nodes has a cost vector with three entries annotated, which represent the three colors. The cost matrices feature infinite costs in their diagonals, because we do not allow two neighboring nodes to get the same color. Any valid coloring corresponds to a PBQP selection with zero costs.
Why is it cool?
The PBQP can be used to model a wide range of real world problems. Usually, if you have a graph and interdependencies, you can use it. Working in compiler construction, i have used PBQP for instruction selection and register allocation.
The reason why such a modelling is attractive is that there is solver algorithm, which takes linear time (relative to the number of edges) and produces near optimal results for sparse graphs. For example, if your graph is a tree, the result will be optimal. There is no theoretical investigation i know of, but the quality of the results seems to be related to the treewidth of the working graph.
Originally, Scholz published the first PBQP solver. Our libFirm compiler contains our implementation of a PBQP solver and features some improvements (infinity propagation, merge reduction).